8장 동적 계획법

8.1 도입

중복되는 부분 문제

동적 계획법(dynamic programming)이란 복잡한 문제를 간단한 여러 개의 문제로 나누어 푸는 방법을 말한다. 하나의 문제를 여러 개의 하위 문제(subproblem)으로 나눠 푸는 접근 방식 자체는 분할 정복(divide and conquer) 알고리즘과 유사하다. 하지만 동적 계획법은 한 하위 문제의 답이 다른 하위 문제를 해결하는 데에 사용되기 때문에 각 문제의 답을 따로 저장하여 시간 효율성을 높인다는 점에서 분할 정복과의 차이를 보인다.

대표적인 예로 동적 계획법을 활용하여 이항 계수(binomial coefficient)를 계산할 수 있다. 이항 계수는 다음과 같은 점화식을 따른다.

위의 점화식을 활용하여 이항계수를 재귀적으로 계산하는 함수를 만든다면 다음과 같다.

int bino(int n, int r) {
    if(r == 0 || n == r) return 1;
    return bino(n-1, r-1) + bino(n-1, r);
}

이 함수를 사용하여 bino(4, 2)를 계산할 때 호출되는 함수를 다음과 같이 트리의 형태로 표현해 보았다.

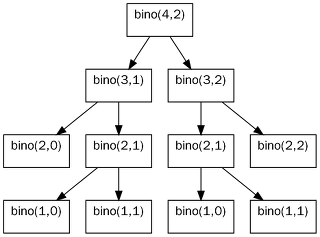
이 트리를 살펴보면 bino(2, 1)이 두 번 호출되고 이로 인해 bino(1, 0)과 bino(1, 1) 또한 자연스레 두 번 호출된다. 두 번 호출된다는 것은 동일한 연산을 두 번 했다는 뜻이며 중복적으로 계산되는 동일한 연산의 값을 따로 저장한다면 똑같은 값을 도출하는 똑같은 연산을 중복적으로 계산하는 낭비를 막을 수 있을 것이다. 중복을 제외한 다음 트리의 함수 호출이 확연히 줄어든 것처럼 말이다.

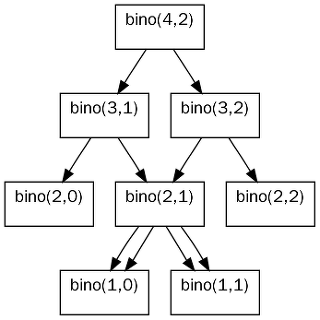
bino(2, 1) 처럼 두 번 이상 계산 되는 부분 문제를 중복되는 부분 문제(overlapping subproblems)라 하며 한 번 계산한 값을 메모리에 저장해 두었다가 중복되는 부분 문제를 반복할 때 재활용하는 최적화 기법을 메모이제이션(memoization)이라 한다. 또한 이 때 이미 계산한 값을 저장해두는 메모리의 장소를 캐시(cache)라 부른다.

메모이제이션을 적용할 수 있는 경우

물론 어느 함수든지 메모이제이션을 적용할 수 있는 것은 아니다.

int counter = 0;
int count() {
    return counter++;
}

함수 외부의 전역 변수 등을 사용하여 결과값에 영향을 주는 함수가 있다면 동일한 입력 값이 주워져도 다른 결과를 반환할 수 있기 때문에 미리 저장해둔 값을 그대로 쓸 수 없게 된다. 즉, 함수의 반환 값이 그 입력 값만으로 결정되는 참조적 투명성(referential transparency)이 보장된 참조적 투명 함수(referenctial transparent function)에게만 메모이제이션을 적용할 수 있다.

예제: 외발 뛰기 (문제 ID: JUMPGAME, 난이도 하)

문제 자세히 보기

// 코드1.
#include <iostream>
#include <cstring>

using namespace std;
int N;
int board[100][100];
int footstep[100][100];

int jumpgame(int x, int y) {
    if(x >= N || y >= N) return 0;
    if(x == N-1 && y == N-1) return 1;
    
    int& jump = footstep[y][x];
    if(jump != -1) return jump;

    return jump = jumpgame(x, y + board[y][x]) || jumpgame(x + board[y][x], y);
}

int main() {
    ios_base::sync_with_stdio(false);
    int C;
    cin >> C;
    while(C--) {
        memset(footstep, -1, sizeof(footstep));
        cin >> N;
        for(int i = 0; i < N; ++i)
            for(int j = 0; j < N; ++j)
                cin >> board[i][j];

        if(jumpgame(0, 0)) cout << "YES" << endl;
        else cout << "NO" << endl;
    }

    return 0;
}

// 코드2.
#include <iostream>
#include <vector>

using namespace std;

bool jumpgame(vector< vector<int> > board) {
    int len = board.size();
    vector< vector<int> > footstep(len, vector<int>(len, 0));

    footstep[0][0] = 1;
    for(int y = 0; y < len; ++y) {
        for(int x = 0; x < len; ++x) {
            if(!footstep[y][x]) continue;

            int jump = board[y][x];
            if(x + jump < len) footstep[y][x + jump] = 1;
            if(y + jump < len) footstep[y + jump][x] = 1;
        }
    }

    return footstep[len - 1][len - 1];
}

int main() {
    ios_base::sync_with_stdio(false);
    int C;
    cin >> C;
    while(C--) {
        int N;
        cin >> N;
        vector< vector<int> > board(N, vector<int>(N));
        for(int i = 0; i < N; ++i)
            for(int j = 0; j < N; ++j)
                cin >> board[i][j];
        
        if(jumpgame(board)) cout << "YES" << endl;
        else cout << "NO" << endl;

    }

    return 0;
}

References

동적계획법 - 위키백과, 우리 모두의 백과사전

Back to top ↑